1)퍼셉트론
퍼셉트론은 인간의 신경세포인 뉴런을 매우 단순히 모사하여 계산 가능한 형태로 만든 알고리즘이다.
퍼셉트론이 하는 일, 국어, 영어, 수학점수, 반영률이 50%, 80%, 30%이라해서
그렇게 가중치를 곱해서 합산한 점수가 100점을 넘으면 시험에 합격하는
것,
이를 수식으로 표현하면,
이때 철수가 시험에서 각각 60, 70, 80점을 받았다면, 가중치 합의 값은
110 = 60*0.5 + 70*0.8 + 80*0.3
으로 100보다 크기 때문에 합격했다고 할 수 있다.
퍼셉트론은 이처럼 선형 분리가능(가중치 합을 이용해 분리가능) 문제를 풀 수 있는 아주 심플한 알고리즘입니다.
2) 비선형 분리 문제
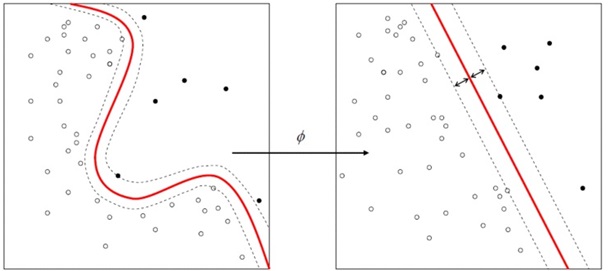
위 그림에서 왼쪽은 비선형 분리가능 문제이고, 오른쪽 그림은 선형
분리가능 문제입니다.
말 그대로 직선만으로 구분이 가능한가, 곡선이 있어야만 구분이 가능한가가
이 둘의 차이입니다.
앞서 살펴본 것과 같이, 퍼셉트론은 선형 분리문제를 풀 수 있는 알고리즘이었습니다.
따라서 성적을 다 더해서 합격, 불합격을 결정하는 아주 쉬운 문제는
풀 수 있었지만
내일 비가 올지 안 올지, 내일의 주가가 오를지 내릴 지와 같은 매우
어려운 문제들은
대부분 비선형 분리가능 문제로 단층 퍼셉트론으로는 풀 수 가 없었습니다.
과거에는 XOR문제라는 가장 간단한 비선형 분리가능 문제가 퍼셉트론의
한계라는 연구가 나오면서 한 때 인공신경망 연구에 겨울이 오기도 했었습니다.
위처럼 XOR 은 1이
한 개 일때에만 1을 내보내는 굉장히 단순한 문제임에도 불구하고 직선 하나로는 0과 1을 나눌 수 없는 문제입니다.
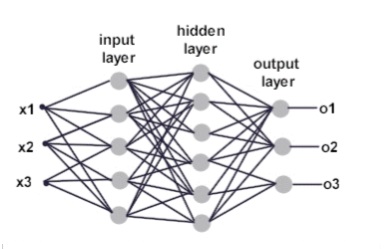
3) 다층 퍼셉트론
그런데 이러한 비선형 분리가능 문제를 여러 층의 퍼셉트론을 쌓으면서 해결할 수 있다는 사실이 알려지면서 또 다시
인공신경망연구가 활발해지기 시작했습니다. 다층퍼셉트론은 간단히 말해
직선을 여러 번 그어서 비선형 분리가능 문제를 해결하려는 개념으로 생각할 수 있습니다.
그래서 이처럼 여러 개의 퍼셉트론을 여러층으로 쌓을 경우 굉장히 복잡한 문제도 해결할 수 있게 된 것.
-관련 키워드
패턴인식, 기계학습, 다층
퍼셉트론을 이용한 XOR 문제 해결, 딥러닝
-Reference
http://blog.naver.com/2011topcit/220510759079